Understanding analytic inverse kinematics
Name:
Due December 2, in lab
This worksheet is intended as a short 60 min exercise to be done in groups of 1-3 people.
Two-link chain inverse kinematics
In this question, you will work through the calculations needed to perform IK for a two-link chain on paper.
Remember that you can use python, octave, matlab, maple, our basecode or any other method to check your answers!
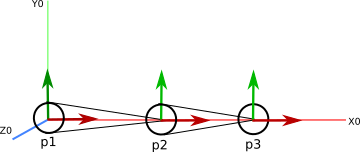
Suppose we have a 2-link chain as in class.
-
The root joint \(p_1\) is located at the origin.
-
The next joint \(p_2\) is offset from \(p_1\) by \((2,0,0)^T\)
-
The next joint \(p_3\) is offset from \(p_2\) by \((5,0,0)^T\)
Reference: IK example
Suppose we wish to position \(p_3\) at a target position \(p_d = (-4,3,0)^T\)
Let’s use the analytic IK method for class to compute rotations for \(p_1\) and \(p_2\) such that \(p_3\) is located at \(p_d\).
-
What is the desired distance r between \(p_3\) and \(p_1\)?
-
What is L1?
-
What is L2?
-
What is the angle \(\theta_{2z}\) that achieves the desired length?
-
What is the new global position of joint 3? Verify that setting the rotation of joint 1 to \(\theta_{2z}\) results in the desired distance.
Use polar coordinates to compute the orientation of joint 1
-
What is the angle \(\theta_{1z}\) that points the limb along the x axis?
-
What is the new global position of joint 3? Verify that setting \(\theta_{2z}\) and \(\theta_{1z}\) points the limb along the x axis using the kinematic equation for our joints.
-
Compute the heading (\(\beta\)) and elevation (\(\gamma\)) that point the limb towards the target \(p_d\).
-
Plug in \(\beta\), \(\gamma\), \(\theta_{1z}\), and \(\theta_{2z}\) and verify that \(p_3\) is now at location \(p_d\).
Find an angle/axis rotation to compute the orientation of joint 1
-
After setting a rotation for joint2, what is the global position of joint 3?
-
What is the direction vector \(r\)?
-
What is the error vector \(e\)?
-
What is the angle \(\phi\) and axis of rotation?
-
Plugin in the angle/axis rotation and \(\theta_{2z}\) and verify that \(p_3\) is now at location \(p_d\)