Understanding transforms
Name:
Due October 28st, in lab
This worksheet is intended as a short 30 min exercise to be done in groups of 1-3 people.
Stacking boxes
A room has three boxes in it. Each box has a local coordinate system attached to it. The lengths of all three boxes in the x,y, and z directions of their local coordinate frames are (3,2,1) respectively. The origin of each box is in the lower left-hand corner. The z-axis of each box is aligned with the global Z axis.
-
The position of B1 with respect to the world (e.g. the coordinate system corresponding to \(X_0, Y_0, Z_0 \)) is \(p_1 = (-2, 0, 1)^T \).
-
The position of B2 with respect to the world is \( p_2 = (4, 0, 2)^T \). The rotation of B2 with respect to the world is 45 degrees around the Z axis.
-
The position of B3 with respect to the world is \( p_3 = (5, 4, 2)^T \). The rotation of B3 with respect to the world is 90 degrees around the Z axis.
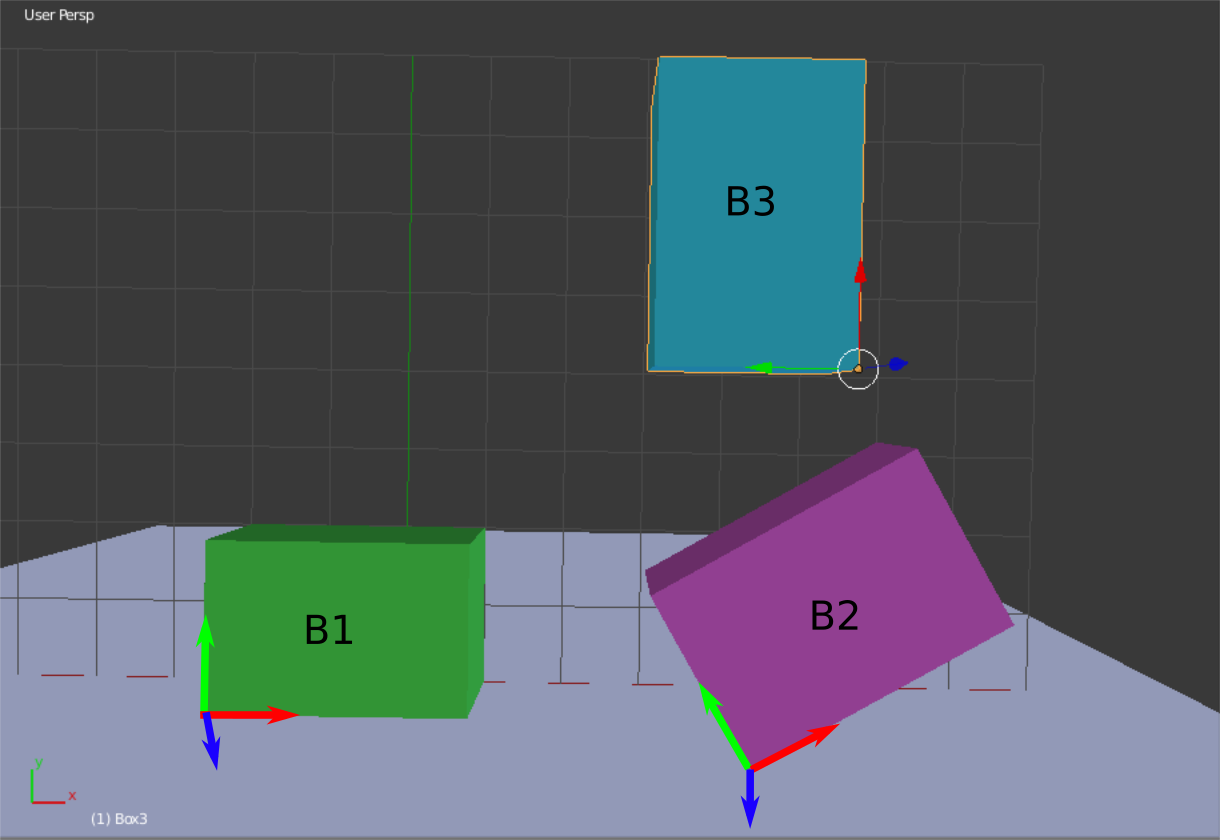
In your assignment for this week, you will implement the solutions of the following questions. In this worksheet, you will manually solve for the transforms corresponding to the above picture.
-
What are the frames of reference — \( F_1^0, F_2^0, F_3^0 \) — in the form of 2x2 block matrices? Each matrix should transform from the block’s local coordinate frame to the global coordinate frame.
-
If a transform \( F_j^i \) transforms from frame j to frame i. The inverse \((F_j^i)^{-1} = F_i^j\) transforms from frame i to frame j. Use this fact to compute the transform from frame 2 to frame 1. You implementation should use \( F_1^0 \) and \(F_2^0 \). What is the position of B2 relative to the local coordinate system attached to box B1? Express your answer as a 4x1 homogeneous coordinate.
-
What is the position of B3 relative to the local coordinate system attached to box B2? Express your answer as a 4x1 homogeneous coordinate.
-
Transforms can be interpreted as (1) conversions between frames of reference, or (2) modifications on an object. Consider Box 2. Suppose we wish to move it from its current location and orientation so it stacks on top of B1. Compute a series of transformations that achieves this result and then multiply them together to find the transformation matrix that stacks B2 onto B1.