Animation Math Review: Self-assessment

Name:

Due September 9

Use the questions below to identify any topics you should review. See the week 01 notes for background information on these topics.

Trigonometry

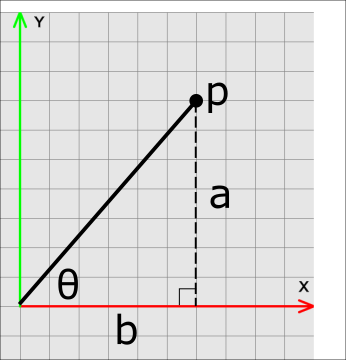
Consider the point p and angle \(\theta\) below, where p is a distance of 1 unit from the origin and \(\theta\) is 45 degrees. What is the coordinate of p? Hint: what are the values of a and b in terms of \(\theta\)?

trig ex1

Consider the point \(p_1\) and angle \(\theta_1\) below. Suppose \(p_1=(2,2,0)^T\). What is the value of \(\theta_1\)? Hint: Use tangent.

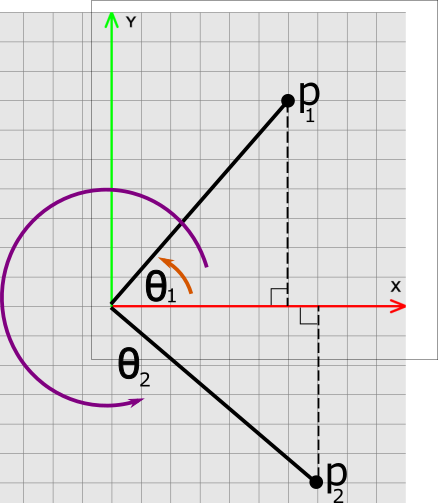
trig ex2

Consider the point \(p_2\) and angle \(\theta_2\) above. Suppose \(p_2=(3,-2,0)^T\). What is the value of \(\theta_2\)? Hint: Use tangent.

 
 
 

Vectors

A vector is an n-tuple of real numbers. In this class, we will work with 2D, 3D, and 4D vectors. Suppose we have a vector u=(-2, 3, 0)T and v=(-1, 4, 0)T.

  • Draw the vectors u and v, with their tails anchored at the origin below.

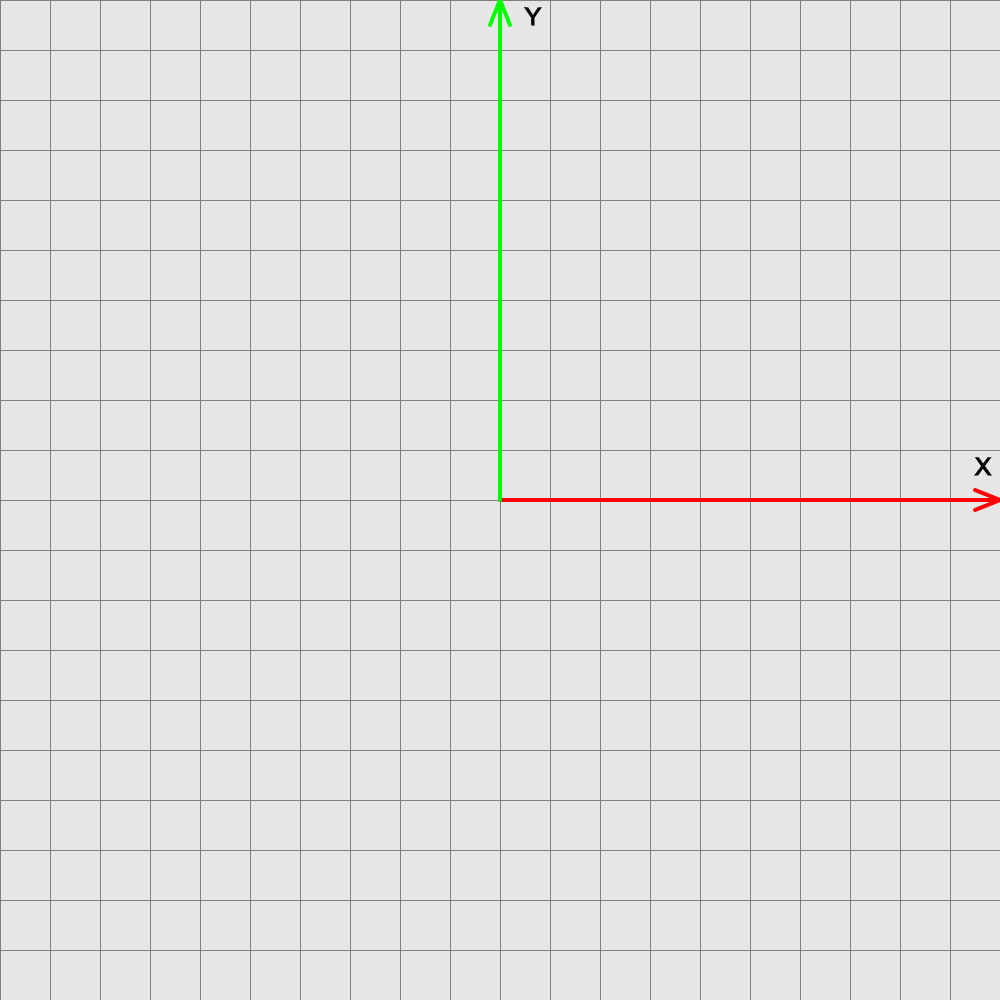
coordinate system

  • What is the length of u?

 
 
 

  • What is the distance between u and v?

 
 
 

  • Compute and draw u + v.

coordinate system

  • Compute and draw u - v

coordinate system

  • Compute the cross product \(u \times v\).

 
 
 

  • Normalize the vector u, e.g. compute \(\frac{u}{\|u\|}\).

 
 
 

  • Compute the dot product \(u \cdot v\).

 
 
 

Matrices

Consider the following matrices

\[A=\begin{bmatrix} 1 & 3 \\ -0.5 & 2 \end{bmatrix}, \quad B = \begin{bmatrix} -3 & 0 \\ 1 & 2 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 3 \\ -4 & 5 \\ 3 & -7 \end{bmatrix}\]

  • What are the dimensions of A, B, and C?

 
 
 

  • What is the transpose of the matric C?

 
 
 

  • Compute the products AB and BA.

 
 
 

  • Is it possible to multiply C times itself? Why not? What about CCT?

 
 
 

  • What is the product of \(AA^{-1}\)?

 
 
 

Consider the following matrix

\[R = \begin{bmatrix} cos(30) & sin(30) & 0\\ -sin(30) & cos(30) & 0\\ 0 & 0 & 1 \end{bmatrix}\]

  • Suppose we have a vector u=(1,0,0)T. Draw u below. Then multiple u by R and draw Ru.

coordinate system

Polynomials

Consider the polynomial \(p(t) = 9t^3 + 6t^2\).

  • What is the degree of \(p(t)\)?

 
 
 

  • What is the derivative of \(p(t)\)?

 
 
 

  • What is the value of \(p(t)\) when t = -1?

 
 
 

Let \(B_0(t) = (t - 1)^2\) and \(B_1 = t - 2\).

  • Compute an expression for \(p(t) = B_0(t) + B_1(t)\) and re-arrange the terms into standard form

Standard form has the following pattern: \(a_nt^n + \ldots + a_2 t^2 + a t + a_0\).